- 2.1 The Difference Quotient Ap Calculus Solver
- 2.1 The Difference Quotient Ap Calculus Frq
- 2.1 The Difference Quotientap Calculus Pdf
- Finding The Difference Quotient
Enter an expression and the variable to differentiate with respect to. Then click the Differentiate button.
The calculator will find the difference quotient for the given function, with steps shown. Show Instructions In general, you can skip the multiplication sign, so `5x` is equivalent to `5.x`. Difference quotient, limit, derivative rules, differentiable, differentiation, continuously differentiable this page updated 19-jul-17 Mathwords: Terms and Formulas from Algebra I to Calculus.
Finding the derivative of
- Math 250 T1-Functions and Di erence Quotients Review Page 1 MATH 250 TOPIC 1 FUNCTIONS AND DIFFERENCE QUOTIENTS I. Evaluating a Function II. Di erence Quotients.
- Calculus, renal: A stone in the kidney (or lower down in the urinary tract). Also called a kidney stone. The stones themselves are called renal caluli. The word 'calculus' (plural: calculi) is the Latin word for pebble. Renal stones are a common cause of blood in the urine and pain in the abdomen, flank, or groin.
involves computing the following limit:
To put it mildly, this calculation would be unpleasant. We would like to find ways to compute derivatives without explicitly using the definition of the derivative as the limit of a difference quotient. A useful preliminary result is the following:
Derivative of a Constant
lf c is any real number and if f(x) = c for all x, then f ' (x) = 0 for all x . That is, the derivative of a constant function is the zero function.
It is easy to see this geometrically. Referring to Figure 1, we see that the graph of the constant function f(x) = c is a horizontal line. Since a horizontal line has slope 0, and the line is its own tangent, it follows that the slope of the tangent line is zero everywhere.
We next give a rule for differentiating f(x) = xn where n is any real number.Some of the following results have already been verified in the previous section, and the
others can be verified by using the definition of the derivative.
This pattern suggests the following general formula for powers of n where n is a positive integer.
Power Rule
In fact, the power rule is valid for any real number n and thus can be used to differentiate a variety of non-polynomial functions. The following example illustrates some applications of the power rule.
Example 1
Differentiate each of the following functions:
(a) Since f(x) = 5, f is a constant function; hence f '(x) = 0.
(b) With n = 15 in the power rule, f '(x) = 15x14
(c) Note that f(x) = x1/2 . Hence, with n = 1/2 in the power rule,
(d) Since f(x) = x-1, it follows from the power rule that f '(x) = -x-2 = -1/x2
The rule for differentiating constant functions and the power rule are explicit differentiation rules. The following rules tell us how to find derivatives of combinations of functions in terms of the derivatives of their constituent parts. In each case, we assume that f '(x) and g'(x) exist and A and B are constants.
The four rules listed above, together with the rule on differentiating constant functions and the power rule, provide us with techniques for differentiating any function that is expressible as a power or root of a quotient of polynomial functions. The next series of examples illustrates this. The linearity rule and the product rule will be justified at the end of the section; a proof of the extended power rule appears in the section on the chain rule.
Example 2 Let
Find f '(x).
Solution Using the linearity rule, we see that
Example 3 Let
Again using linearity,
f'(x) = a(x3)' + b(x2)' + c(x)' + (d)' = 3ax^2 + 2bx + c
Example 3 can be generalized as follows:
A polynomial of degree n has a derivative everywhere, and the derivative is a polynomial of degree (n - 1).
Example 4 Let
Find f '(x).
First we use the product rule, since f(x) is given as the product of x2 and x2 -x + 1:
2.1 The Difference Quotient Ap Calculus Solver
The difference quotient is a formula that finds the average rate of change of any function between two points. In calculus, the difference quotient is the formula used for finding the derivative, which is the limit of the difference quotient between two points as they get closer and closer to each other (this limit is also the rate of change of a function at a single point). The difference quotient was formulated by Isaac Newton.
Definition[change | change source]
Introduction[change | change source]
The difference quotient can be described as the formula for finding the slope of a line that touches a curve at only two points (this line is called the secant line). If we are trying to find the slope of a perfectly straight line, then we use the slope formula, which is simply the change in y divided by the change in x. This is very accurate, but only for straight lines. The difference quotient, however, allows one to find the slope of any line or curve at any single point. The difference quotient, as well as the slope formula, is merely the change in y divided by the change in x. The only difference is that in the slope formula, y is used as the y-axis, but in the difference quotient, the change in the y-axis is described by f(x). (For a detailed description, see the following section.)
Mathematical definition[change | change source]
The difference quotient is the slope of the secant line between two points.
If one uses the notation x2=x1+Δx{displaystyle x_{2}=x_{1}+Delta x}, then this becomes m=f(x+Δx)−f(x)(x+Δx)−x1=f(x+Δx)−f(x)Δx{displaystyle m={frac {f(x+Delta x)-f(x)}{(x+Delta x)-x_{1}}}={frac {f(x+Delta x)-f(x)}{Delta x}}}.
(here, Δx{displaystyle Delta x} is called the limiting variable of the difference quotient. Other variables, such as δx{displaystyle delta x} and h{displaystyle h}, are used as well.[1][2][3])
The difference quotient can be used to find the slope of a curve, as well as the slope of a straight line. After we find the difference quotient of a function and take the limit as two points get closer and closer to each other, we have a new function, called the derivative. To find the slope of the curve or line, we input the value of x to get the slope. The process of finding the derivative via the difference quotient is called differentiation.
2.1 The Difference Quotient Ap Calculus Frq
Applications of the difference quotient (and the derivative)[change | change source]
The derivative has many real life applications. One application of the derivative is listed below.
2.1 The Difference Quotientap Calculus Pdf
Physics[change | change source]
In physics, the instantaneous velocity of an object (the velocity at an instance in time) is defined as the derivative of the position of the object (as function of time). For example, if an object's position is given by x(t)=-16t2+16t+32, then the object's velocity is v(t)=-32t+16. To find the instantaneous acceleration, one simply takes the derivative of the instantaneous velocity function. For example, in the above function, the acceleration function is a(t) = -32.
Related pages[change | change source]
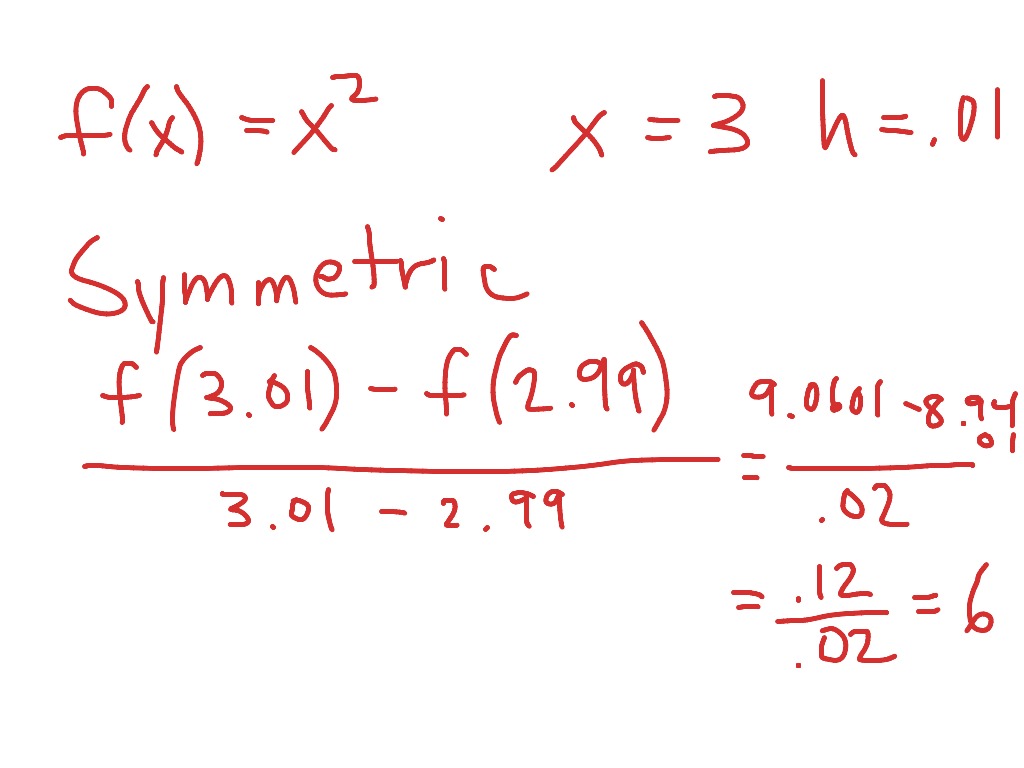
Applications of the difference quotient (and the derivative)[change | change source]
The derivative has many real life applications. One application of the derivative is listed below.
2.1 The Difference Quotientap Calculus Pdf
Physics[change | change source]
In physics, the instantaneous velocity of an object (the velocity at an instance in time) is defined as the derivative of the position of the object (as function of time). For example, if an object's position is given by x(t)=-16t2+16t+32, then the object's velocity is v(t)=-32t+16. To find the instantaneous acceleration, one simply takes the derivative of the instantaneous velocity function. For example, in the above function, the acceleration function is a(t) = -32.
Related pages[change | change source]
References[change | change source]
- ↑'List of Calculus and Analysis Symbols'. Math Vault. 2020-05-11. Retrieved 2020-10-14.
- ↑'Mathwords: Difference Quotient'. www.mathwords.com. Retrieved 2020-10-14.
- ↑'Difference Quotient'. www.analyzemath.com. Retrieved 2020-10-14.
